---

Learning Objectives

• Learn how to use Affine transforms

• Differentiate translate, rotate, skew, shear

Review

• Data Structures

• Vector Data

• Raster Data

• Matrix Algebra Intro

---

Affine Transforms

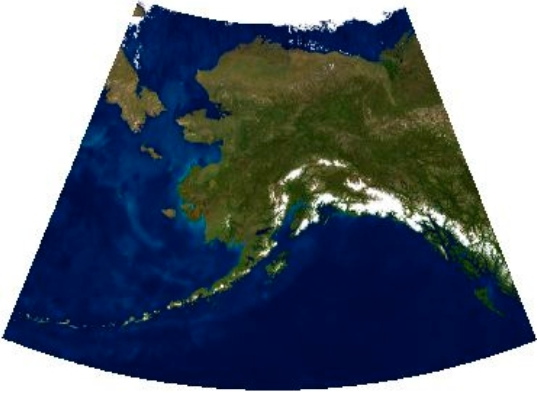
Affine transformations allows us to use simple systems of linear equations to manipulate any point or set of points. It allows us to move, stretch, or even rotate a point or set of points. In the case of GIS, it is used to distort raster data, for instance satellite imagery, to fit a new projection or CRS.

First some general properties of affine transforms:

• Preserves

  • Points, straight linear & planes

  • Sets of parallel lines

  • Ratio of distances between points on same straight line

• Distorts

  • Angle between lines

  • Distance between points

Types of Transformations

There are four core ways that you can manipulate an image. These are called “Transforms”:

Transform	Description	Example
Translation	Moves a set of points some fixed distance in the x and y plane
Scale	Increases or decreases the scale, or distance between points in the x and y plane
Rotate	Rotates points around the origin, or some defined axis
Shear	Shifts points in proportion to any given points x and y coordinate
Image Credit: Wikipedia

In combination we can warp any point, or set of points (e.g. raster image) into a new projection. This is the equivalent of reprojection for vector data. In order to implement these transforms we will need to learn about the math behind Affine Transforms! Yeah!

Simple Transform Examples

To simplify things first lets think about how to do transformations of a single point in a 2d space.

For any location \( \mathbf{x} = (x,y)\) we can transform \( \mathbf{x} \) to \(\mathbf{\acute{x}}\) using simple linear adjustments. Here we can think of point \(\mathbf{x}\) as being stored as an array:

\[\begin{split} \begin{eqnarray} \mathbf{x} = \left[ \begin{array}{cc|r}x \\ y \end{array} \right] \mbox{can be transformed to } \mathbf{\acute{x}} = \left[ \begin{array}{cc|r}\acute{x} \\ \acute{y} \end{array} \right] \end{eqnarray} \end{split}\]

From here we can transform the values in the \(x\) and \(y\) position using scaler values \(a\) through \(f\):

\[\begin{split} \begin{eqnarray} \mathbf{\acute{x}} = \left[ \begin{array}{cc|r}ax+by+c \\ dx+ey+f \end{array} \right] \end{eqnarray} \end{split}\]

Note

Looking at the formula above, we are adjusting the value of \(x\) with \(ax+by+c\), so \(x\) can be multiplied (scaled) by some value \(a\), it can also be scaled based on the \(y\) value with \(+ by\), or simply adjusted up or down by the value \(+ c\)

To understand how this works, let’s walk through the basic transformations of \(\mathbf{x}\):

If we multiply \(x\) and \(y\) by one, by setting \(a,e = 1\), and zero out the effect of the other axis, by setting \(b,d = 0\), we have a simple case of translation, where \(x\) moves right by \(c\) and \(y\) up by the value of \(f\):

\[\begin{split} \begin{eqnarray} \mathbf{\acute{x}} = \left[ \begin{array}{cc|r}1x+0y+c \\ 0x+1y+f \end{array} \right] \end{eqnarray} \end{split}\]

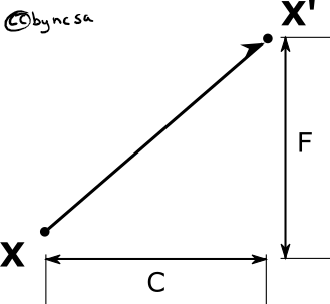
Fig. 33 Translate a coordinate

We can scale \(x\) and \(y\) by setting \(a\) and \(e\) to 0.5 (or some fraction), and setting all other values to zero (\(b,d,c,f = 0\)):

\[\begin{split} \begin{eqnarray} \mathbf{\acute{x}} = \left[ \begin{array}{cc|r}ax \\ ey \end{array} \right] \end{eqnarray} \end{split}\]

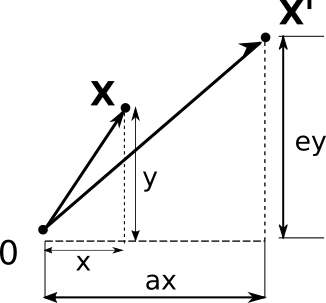
Fig. 34 Scale a coordinate

We can rotate a point around the origin by setting \(a,e = \cos\theta\), \(b = -\sin\theta\) and \(c,f = 0\):

\[\begin{split} \begin{eqnarray} \mathbf{\acute{x}} = \left[ \begin{array}{cc|r} x\cos\theta - y\sin\theta \\ x\sin\theta+y\cos\theta \end{array} \right] \end{eqnarray} \end{split}\]

where \(\theta\) is the angle of rotation (counterclockwise) around the origin.

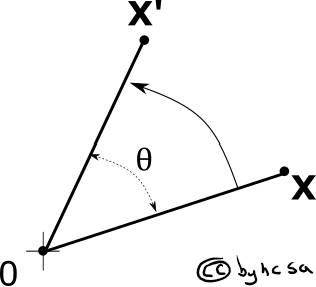
Fig. 35 Rotate a coordinate

Finally by adjusting \(x\) based on the value of \(y\) (and visa versa), we can achieve a shear transform:

\[\begin{split} \begin{eqnarray} \mathbf{\acute{x}} = \left[ \begin{array}{cc|r} x+by \\ y+dx \end{array} \right] \end{eqnarray} \end{split}\]

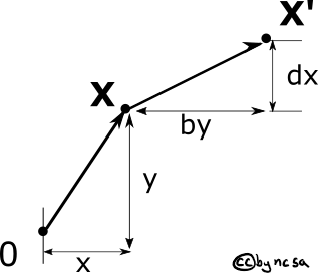
Fig. 36 Shear transform a coordinate

Transforming Matrices

It is often convenient to represent these equations as matrices. This allows us to easily chain together a series of operations. We can represent our transformed point \(\mathbf{\acute{x}}\) as follows:

\[\begin{split} \begin{eqnarray} \left[ \begin{array}{cc|r} \acute{x} \\ \acute{y} \end{array} \right] = \left[ \begin{array}{cc|r} ax+by \\ dx+ey \end{array} \right] = \left[ \begin{array}{cc|r} a \ \ b \\ d \ \ e \end{array} \right] \left[ \begin{array}{cc|r} x \\ y \end{array} \right] \end{eqnarray} \end{split}\]

Note

If you aren’t familiar with how matrix multiplication works please watch this.

In this new context we can easily do a scale, rotate or shear transform by replacing the matrix of \(a,b,d,e\) with:

\[\begin{split} \begin{eqnarray} \mbox{Rotate: } \left[ \begin{array}{cc|r} \cos\theta \ \ -\sin\theta \\ \sin\theta \ \ \cos\theta \end{array} \right] \end{eqnarray} \end{split}\]

\[\begin{split} \begin{eqnarray} \mbox{Scale: } \left[ \begin{array}{cc|r} S_{x} \ \ 0 \\ 0 \ \ S_{y} \end{array} \right] \end{eqnarray} \end{split}\]

\[\begin{split} \begin{eqnarray} \mbox{Shear: } \left[ \begin{array}{cc|r} 1 \ \ r_{x} \\ r_{y} \ \ 1 \end{array} \right] \end{eqnarray} \end{split}\]

But wait, what about the easiest transform, “translation”? Unfortunately that makes things a little more complicated! But not that complicated.

In order to be able to perform a translate in matrix form we need to extend our matrices, adding one row along the bottom. In the following form we can now perform all the basic transformations to calculate \( \mathbf{\acute{x}}\):

\[\begin{split} \begin{eqnarray} \left[ \begin{array}{cc|r} \acute{x} \\ \acute{y} \\ 1 \end{array} \right] = \left[ \begin{array}{cc|r} a \ \ b \ \ c \\ d \ \ e \ \ f \\ 0 \ \ 0 \ \ 1 \end{array} \right] \left[ \begin{array}{cc|r} x \\ y \\ 1 \end{array} \right] = \left[ \begin{array}{cc|r} ax+by+c \\ dx+ey+f \\ 1 \end{array} \right] \end{eqnarray} \end{split}\]

Now that we have scalers \(c\) and \(f\) all the transforms are possible. We do however, need to update our previous operations:

\[\begin{split} \begin{eqnarray} \mbox{Translate: } \begin{bmatrix} 1 & 0 & \Delta x \\ 0 & 1 & \Delta y \\ 0 & 0 & 1 \end{bmatrix} \end{eqnarray} \end{split}\]

Where \(\Delta x\) shifts in the \(x\) axis and \(\Delta y\) determines the shift in the \(y\) axis.

\[\begin{split} \begin{eqnarray} \mbox{Rotate: } \begin{bmatrix} \cos\theta & -\sin\theta & 0 \\ \sin\theta & \cos\theta & 0 \\ 0 & 0 & 1 \end{bmatrix} \end{eqnarray} \end{split}\]

\[\begin{split} \begin{eqnarray} \mbox{Scale: } \begin{bmatrix} S_{x} & 0 & 0 \\ 0 & S_{y} & 0 \\ 0 & 0 & 1 \end{bmatrix} \end{eqnarray} \end{split}\]

\[\begin{split} \begin{eqnarray} \mbox{Shear: } \begin{bmatrix} 1 & r_{x} & 0 \\ r_{y} & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} \end{eqnarray} \end{split}\]

Numeric Examples

Translate

Now let’s assume we have a point a at (-2,-2) for (x,y). For simplicity sake lets assume we want to move it up to the origin by adding 2 to both x and y.

Let’s start by defining our point in our matrix form:

\[\begin{split} \begin{eqnarray} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} = \begin{bmatrix} -2 \\ -2 \\ 1 \end{bmatrix} \end{eqnarray} \end{split}\]

Let’s get our transform matrix \(M\) to perform our translate, where \(\Delta x, \Delta y = 2\) because we want to move it up and to the right:

\[\begin{split} \begin{eqnarray} \begin{bmatrix} 1 & 0 & 2 \\ 0 & 1 & 2 \\ 0 & 0 & 1 \end{bmatrix} \end{eqnarray} \end{split}\]

We can then multiply the two:

\[\begin{split} \begin{eqnarray} \begin{bmatrix} 1 & 0 & 2 \\ 0 & 1 & 2 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} -2 \\ -2 \\ 1 \end{bmatrix} = \begin{bmatrix} -2 \times 1 + -2 \times 0 + 1 \times 2 \\ -2 \times 0 + -2 \times 1 + 1 \times 2 \\ -2 \times 0 + -2 \times 0 + 1 \times 1 \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix} \end{eqnarray} \end{split}\]

Congrats you reached (0,0), just like you always dreamed!

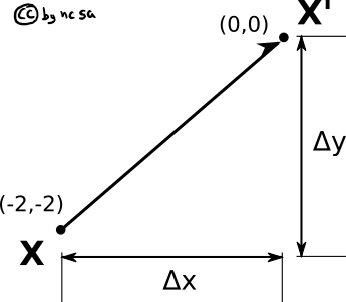
Fig. 37 Moving a point

Note

Remember the bottom row can be ignored because \( \begin{bmatrix} x \\ y \\ 1 \end{bmatrix}\)

Rotate

All the transformations follow the same procedure, let’s try rotation just to make sure that we have it figured out. Let’s rotate our point at (-2,-2) by 180 degrees around the origin:

\[\begin{split} \begin{eqnarray} \begin{bmatrix} \cos{180} & -\sin{180} & 0 \\ \sin{180} & \cos{180} & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} -2 \\ -2 \\ 1 \end{bmatrix} = \end{eqnarray} \end{split}\]

\[\begin{split} \begin{eqnarray} \begin{bmatrix} -2 \times \cos{180} + -2 \times -\sin{180} + 1 \times 0 \\ -2 \times \sin{180} + -2 \times \cos{180} + 1 \times 0 \\ 1 \times 0 + 1 \times 0 + 1 \times 1 \end{bmatrix} = \begin{bmatrix} 2 \\ 2 \\ 1 \end{bmatrix} \end{eqnarray} \end{split}\]

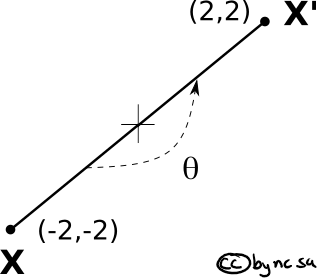
Fig. 38 Rotate a point